This article is about using Fortune’s Algorithm to generate Voronoi Diagrams in O(nlogn) time. If I’d known how hard it would be I wouldn’t have started it. If you are intending to implement it with the intent to actually use it, rather than as an exercise, I would recommend not using Fortune’s. Unless you are doing a lot of large diagrams - like multiple large diagrams every second - I’d suggest looking at an O(n^2) implementation, which I’ve heard is much easier. Or even better, using a library. While it was very frustrating at times, it is a cool looking algorithm when you get it working.
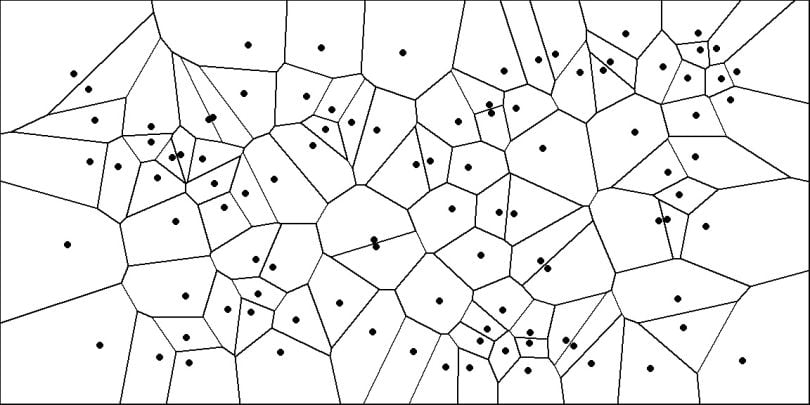
A Voronoi diagram is method of partitioning a plane into regions. It is often used to procedurally generate maps.

You pick a bunch of points on a plane called ‘sites’, and the region, or ‘cell’, corresponding to that site is the area enclosing every point which is closer to that site than to any other site.
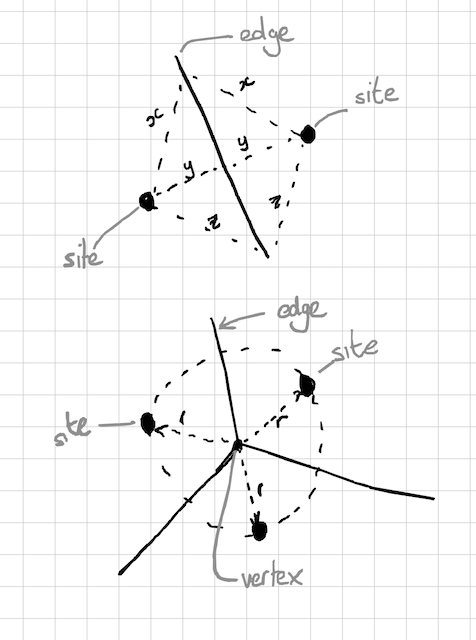
Put another way, the edge of each cell is where it is equidistant to two sites (top drawing). The ‘corners’ of the cells, where edges meet, are called ‘Voronoi Vertices’. These are the points which are equidistant from three sites (bottom drawing).
There are a few methods for generating the diagrams. A popular one is Fortune’s Algorithm, and that’s the one I’ll describe here.
Seen visually, this method creates a line which ‘sweeps’ from the left edge of the plane to the right, pixel by pixel - called the sweep-line. When the line encounters a site it creates what looks like a ‘bubble’ around it (actually, a parabolic arc). The bubble grows as the sweep line gets further away. The magic happens when two arcs from two different sites collide: the point of collision becomes the edge of the cells, it being equidistant between the two points. And when two of those edges collide, it creates a corner in the diagram. The ‘frontier’ of all the active bubbles is called the beachline, I guess because it sort of looks like a coast?

In reality you don’t actually go pixel by pixel. Interesting things happen at certain points which can be calculated - irritatingly called events - and we just look at those. There’s a lot to unpack here, and we need to do some groundwork before really getting into it.
There are a few terms that are core to understanding the process. I’ll define them briefly here, but most of them won’t make sense until you understand how they relate to the algorithm. they’re just here for reference so you can come back to them later.
A site, sometimes called a seed, is a 2d point. The sites are what determine the shape of the resulting Voronoi diagram, because the edges of the cells are equidistant from two sites.
The sweep line is the vertical line that sweeps across the region. As the sweep line passes each event in the event queue, that event is processed.
The beach line is a line comprised of a series of arcs. When an event is processed, the beach line is affected by either adding or removing arcs. Each arc corresponds to a site, though each site can have multiple, or no, arcs on the beachline at any given point in time.
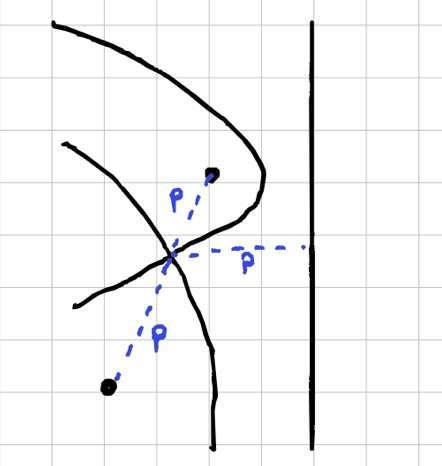
An intersection is a point where two arcs on the beachline meet eachother. These intersections are also equidistant between the sites to which the arcs relate.
The event queue is where the site and circle events are stored, ordered by ascending x-coordinate. The algorithm progresses by popping the next event off the queue, and processing it, until there are none left. This is a conceptually a priority queue, though isn’t implemented as one here.
A site event is one of the two types of event on the event queue, and the simpler one. It is defined by the coordinates of a corresponding site. Processing a site event results in a new arc being added to the beach line. Since the sites are known when you begin the algorithm, they are added to the queue before the algorithm starts processing events.
A circle event is the other type of event on the queue. It is defined by the three arcs which sit on the perimeter of the circle. Apart from the center and radius of the circle, another important attribute of the circle is the circle point, which is the right-most point of the circle. It’s the x-coordinate of this circle point which determines where it sits in the event queue. Circle points are not known ahead of time, but are generated as arcs are added to or removed from the beach line. Processing a circle event results in an arc being removed from the beach line, and a Voronoi Vertex and two half edges being created.
A Voronoi Vertex is a point equidistant between 3 sites, where three equiedges meet. They are the corners of the cells of the Voronoi diagram. They are also the center of the circles of circle events.
An equiedge is an line which is equidistant between two sites in the Voronoi diagram.
An incomplete edge is a line which has a fixed point on one side, but the other side is defined as the intersection of two parabola focus points. Since the parabola intersections change with the sweep line, this end of the edge is not fixed. Incomplete edges become ‘complete’ when the two incomplete edges meet eachother (at a circle event), and in doing so generate Voronoi Vertices and half edges.
A half edge is a part of the Voronoi data structure. It has a origin point (a Voronoi Vertex) and a ‘twin’ half edge. Half edges are generated from the ‘completion’ of an incomplete edge.
The concept and properties of a parabola are really important to this
algorithm. So we need to be able to represent
parabola.1
1 https://en.wikipedia.org/wiki/Parabola
Parabola are usually defined using an equation y=ax^2+bx+c
or some slight variation on that. We use a different, but equivalent
formulation called the ‘locus definition’. You can define a parabola
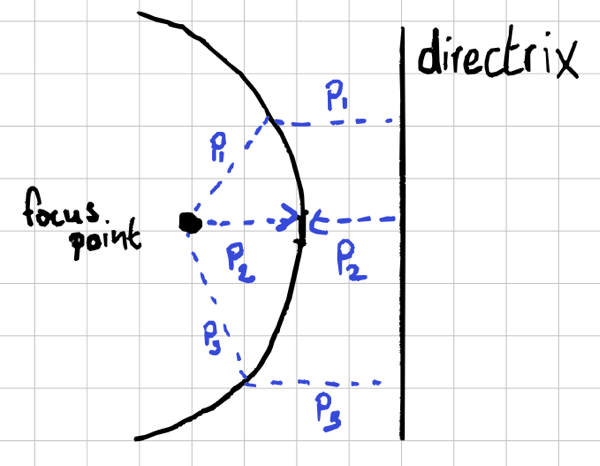
using two things: A 2d coordinate called the focus
point, and a line called the
directrix2
2 You’ll
often see this formulated as a ‘vertex’ and ’focal length. I’m
not going to go into detail here, but they are almost completely the
same. The focus point/directrix method is just a bit more convenient for
our purposes. .
The parabola consists of all points which are equally distant from the
focus point and the directrix. If we restrict ourselves to a vertical
directrix, then the directrix becomes a single number representing the
x-coordinate of the line.
This how you can calculate the points of the parabola. Derivation is not going to be covered here, and it’s not actually important for the algorithm. But it’s useful for drawing it3 3 This is pseudocode, though a very pythony one .
def parabola_x(focus:Vector2, y: int, d: int):
x = y - focus.y
x *= x
x /= focus.x - d
x += focus.x + d
x *= 0.5
return x
def draw_parabola(f:V2, d:int, y0:=0, yn:=HEIGHT, color:=BLACK)
for y in y0..<yn:
DrawPixel(parabola_x(f, y, d), y, color)
focus_point = [200,300]
directrix = 300
# The focus point
draw_circle(focus_point, 5, RED)
# The directrix/sweep line
draw_line([directrix, 0], [directrix, H] 5, BLUE)
draw_parabola(focus_point, directrix)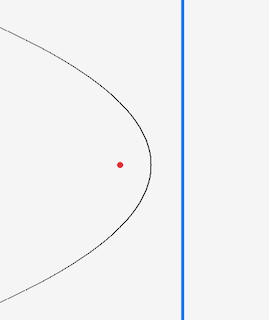
Let’s tie all this back to the problem: Remember the goal here is to find the equiedge between two sites - the line that has all points that are the same distance from both sites. The benefit of defining a parabola like this is that, if we set the focus points to be our sites and the directrix to be our sweep line, then:
So by finding the interections between two parabola you find the ‘boundary’ edge which is equidistance from both sites4 4 the Intersection function I use here is just some not very difficult math which you can get by using the quadratic formula for the two parabola, after converting from the locus definition to the algebraic one .
# Coordinates of two sites
site1 = [200, 300]
site2 = [400, 700]
# X coord of sweeplines at progressive points
sweep_lines = [450, 500, 600, 700, 800, 900]
# Intersection fn takes 2 sites and a sweep line, returns
# intersections.
start, _ = intersection(site1, site2, sweep_lines[0])
end, _ = intersection(site1, site2, sweep_lines[len(sweep_lines)-1])
draw_circle(site1, 5, RED)
draw_circle(site2, 5, RED)
for s in sweep_lines:
draw_parabola(site1, s, color=GREEN)
draw_parabola(site2, s, color=BLUE)
draw_line(start, end, 5, ORANGE)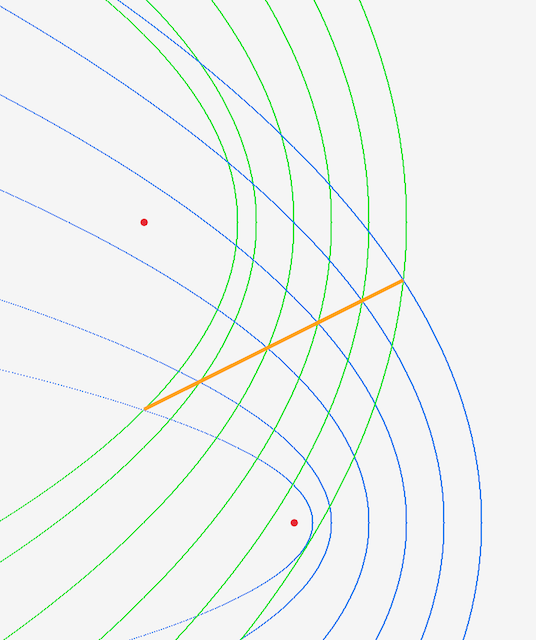
This is math magic, I love it.
The beachline is like the ‘frontier’ of all the arcs at a given point
in the sweep line. The first takeaway from this is that, since the sweep
line is going to be the same for all arcs, we can represent an arc just
by its focus point (i.e. the site). And since the focus points are our
sites, every ‘arc’ on the beachline is just the 2d coordinate of one of
our sites. The second takeaway is that we can represent the frontier
line as a simple sequence of
points5
5 I’m
just going to represent it as a vector, which does make a few things
inefficient. A binary tree would be better. But this is fine for small
implementations .
So in the following, the beachline is arc 1 and arc 2. Or,
[arc1,arc2]
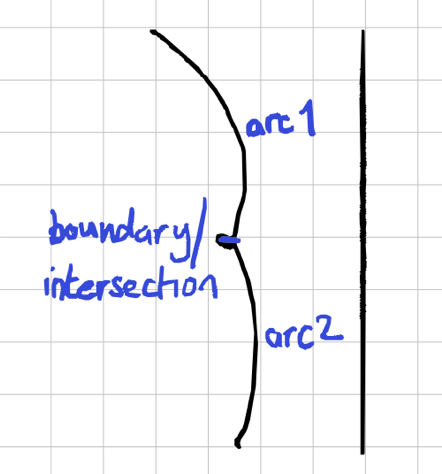
And here it’s [arc1, arc2, arc3]
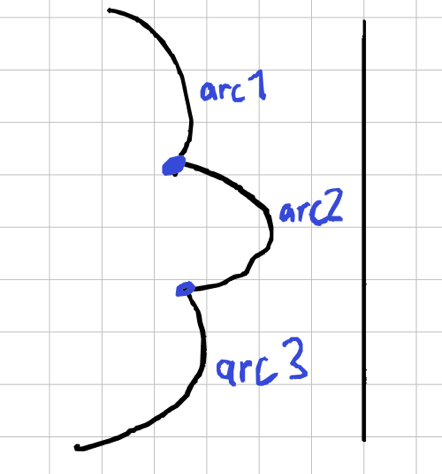
There are a few nuances though. Look at this one, where there are three arcs: 1, 2, and 3. A full description of the frontier needs to reflect that 2 separate parts of arc1 are on the frontier, with the middle bit being covered by 3.
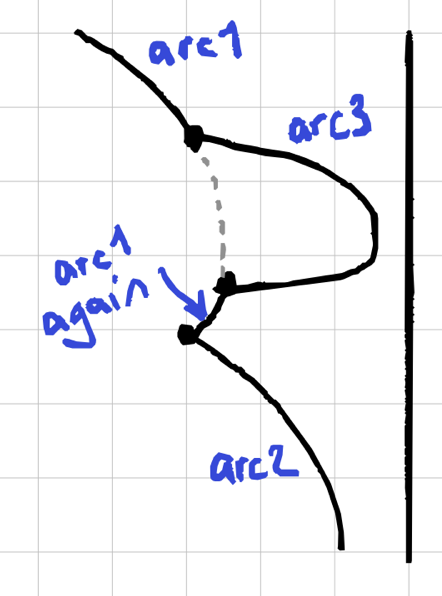
It’s actually easy to handle this: just put it in the beachline
twice: [arc1, arc3, arc1, arc2]
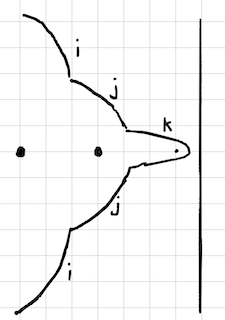
A final scenario I’ll mention, because it turns out to be important,
is that it’s totally possible to have a beachline where the same three
arcs appear together but in a different order. Like you might
have the sequence [i,j,k], and then later
[k,j,i]. Triples of arcs on the beachline are important for
reasons that will become clear. Each ordered triple will be
unique in the beachline. So you can’t have [i,j,k]
twice.
For each pair of arcs in the beachline we calculate the intersection, and by drawing the arcs between the intersection, we sketch the beachline.
def draw_beachline(beachline:[V2], d:int)
y = 0
for i in 0..<len(beachline)-1
p1, _ = intersection(beachline[i], beachline[i+1], d)
draw_parabola(beachline[i], d, y, p1.y)
y = p1.y
draw_parabola(beachline[len(beachline)-1], d, y, H)
site1 = [200, 300]
site2 = [400, 700]
site3 = [450, H/3]
sweep = 500
beach_line = [site1, site3, site1, site2]
draw_circle(site1, 5, RED)
draw_circle(site2, 5, RED)
draw_circle(site3, 5, RED)
draw_line([sweep, 0], [sweep, H], 5, BLUE)
draw_beachline(beach_line, sweep)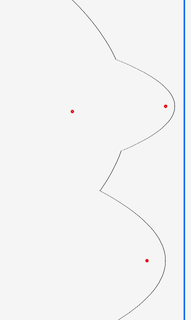
So that’s the beachline: just a sequence of points, where each point represents both a site and an arc. Next we should talk about how things get added to and removed from the beachline. I mentioned at the beginning that interesting stuff happens at some special points on the sweep line. The first of these is when the sweep line hits a new site. This creates a new arc, and inserts it into the sequence, ‘splitting’ the old arc in two. Inserts where? You need to find the arc which, if you draw a line left from the new site, you hit. That’s the arc that gets split. It’s easier to see it in a picture.
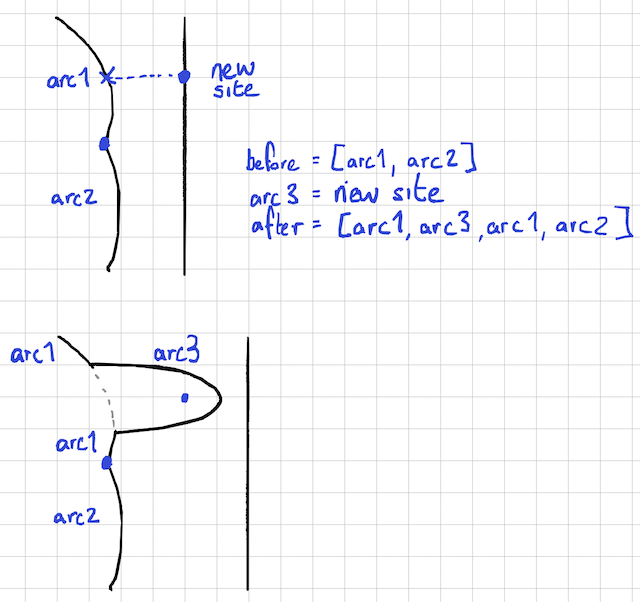
def add_site(beachline:[V2], site:V2):
if len(beachline) == 0:
append(beachline, site)
return
sweep = site.x
insert_after = 0
for i in 0..<len(beachline)-1:
b, _ := intersection(beachline[i], beachline[i+1], sweep)
if b.y > site.y:
insert_after = i
break
inject_at(beachline, insert_after+1, site)
inject_at(beachline, insert_after+2, beachline[insert_after])
site1 = [200, 300]
site2 = [400, 700]
site3 = [450, 280]
beach_line : []
add_site(beach_line, site1)
add_site(beach_line, site2)
add_site(beach_line, site3)
print(beach_line)
## =>
[[200, 300], [450, 280], [200, 300], [400, 700], [200, 300]]
# site1 site3 site1 site2 site1As you can see from this, we add sites to the beach line from left to right by the x-coordinate. Since we know the sites from the beginning, we can put them in a queue and ‘pop’ them off off one at a time. That’s why in the literature they’re called site events, though I don’t like that much.
Here’s what the beachline looks like after processing these three sites events in order:
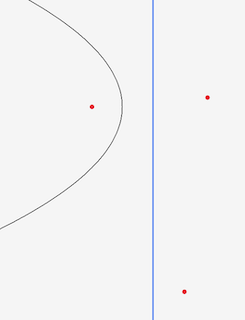
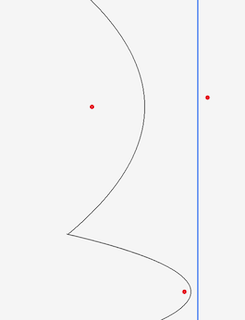
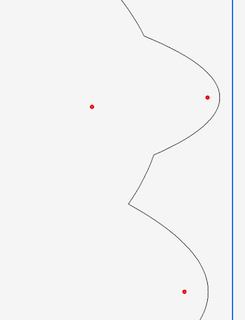
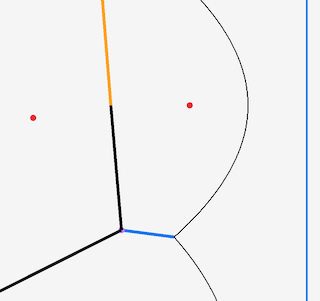
After we’ve processed the sites and draw the the beachline we see something like this6 6 I added an orange line which shows the equiedge between the respective sites .
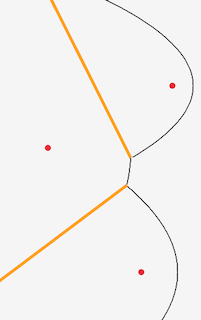
All good. If we carry on though, and draw the beachline with the sweep line a bit further on, we run into a problem.
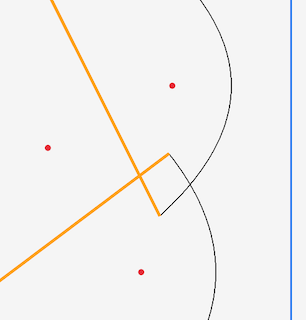
We went too far! If I dial that line back a bit, you can see what is happening - or about to happen - more clearly:
Depending on how you look at it, 3 things are happening:
So when we get to that point we need to remove the middle arc from the beachline. This ‘arc squeezing’ point is the second type of point we need to deal with, but its a bit more complicated than the sites. So lets look at what’s happening in more detail.
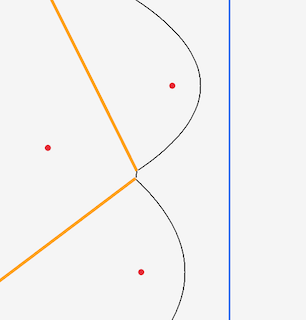
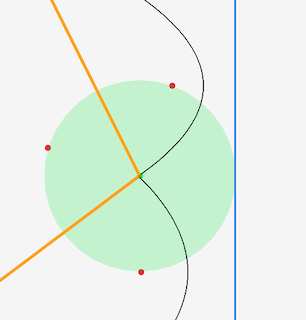
Way back at the start I said the edges of the Voronoi were where two points were equidistant, and the ‘corners’ of the cells where the edges meet are the points which are equidistant from 3 or more sites. If you eyeball it in the above picture, you can see that it looks like the where the lines intersect is about in the middle of the three points.
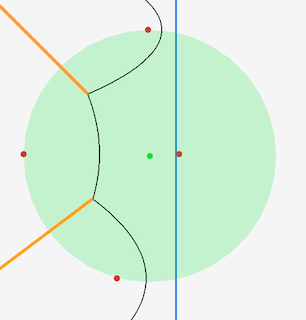
We can be a bit more precise than that. What we’re saying mathematically is that, if we draw a circle where the 3 sites all sit on the radius, the center of the circle will be equidistant from all 3 points, and by the above definition will be where the edges of the Voronoi intersect. A circle which puts a set of given points on its circumference is called a circumcircle (and it’s center is a circumcenter)7 7 https://en.wikipedia.org/wiki/Circumcircle. The math for calculating the center and radius of the circle can be taken straight from here. . If we plug the numbers in and draw the circle we get this:
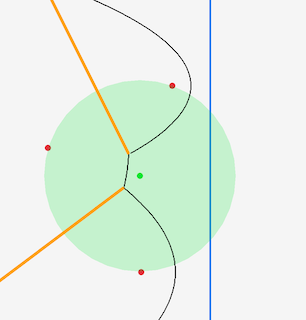
Which is spot on. And this is the really important point, because
this is where we finally have a Voronoi Vertex, which is the
whole point of this exercise. When we reach the Voronoi Vertex, defined
by the three arcs on the beachline [..,i,j,k,..], the
center arc j gets removed from the beachline, so the
beachline looks like [..,i,k,..]. So now we have a new
boundary between arcs i and k, where none existed
before. You can see how this looks in the diagram: there’s a new
equiedge coming out of the Voronoi Vertex we created, which is between
sites i and k
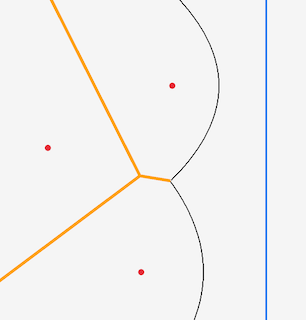
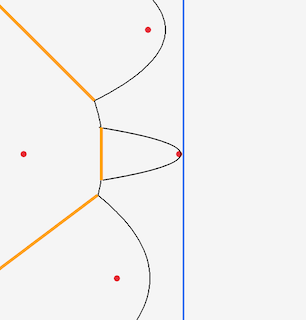
But we’re not out of the woods yet. We know we we need to process each site (i.e. add a new arc) in order from left to right. And that when we find an intersection, we need to process that intersection (remove the arc from the beachline, record a Voronoi vertex.) But when in the sequence of points can we do that? You might think, as soon as we know those 3 points, we can calculate the circle and therefore the intersection. But that won’t work. To see why, consider the following scenario. The first picture is the same scenario we saw before, and you might think you can go ahead and assume that the edges will converge. But wait! There is another site, and the sweep line hits it before the edges converge, breaking up the arc before it reaches the intersection point.
The important thing is that the new site is inside the circle. And that is the answer to the question: You process the edge intersection when the sweepline leaves the circle without having encountered any sites inside the circle. The point where the sweepline leaves the circle is the right-most point of the circle - called the circle point.
Until now we’ve been sequentially processing site events. Now we need to add this second type of event, called a circle event for obvious reasons. Every time we change the beachline, we need to check for new circle events, and check existing circle events to see if they are still valid. This is probably the hardest concept in the algorithm to grok, so I’m going to spend some time on it, before talking about what happens when our sweepline passes a circle point.
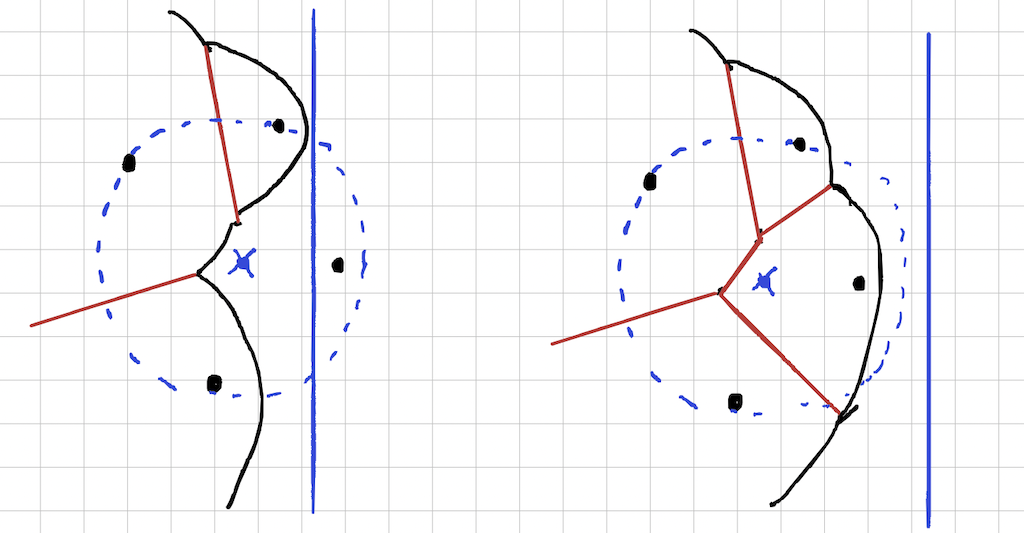
Say you have a beachline containing the three arcs
[..,i,j,k,..]. Because arcs are references to sites
(remember, an ‘arc’ in our datamodel is just a 2d point, with each 2d
point being a site.) i,j and k in addition to being
arcs are also sites. The significance of them being next to eachother in
the beachline is that the equiedges between i and j, and j and k,
could intercept at the center of the circumcircle they
describe, becoming a Voronoi Vertex. This is what a circle event really
is: A reference to a triple of arcs on the beachline (not every
triple on the beachline, but we’ll park that for now).
If there is a change to the beachline affecting that triple before
those lines intersect, then there is no intersection. When I say
‘change’, I mean either a new arc added to the beachline by a site
parameter or one has been removed. In the case of an addition, the
beachline becomes [..,i,j,L,j,k,..]. The triple
i,j,k has gone - and so has any circle event associated with
it. And there are two new triples i,j,L and L,j,k. So
we need to check both of those to see if they create generate circle
events. That’s what happened in the following picture: the arc which is
being ‘squeezed’ is actually being split by the arc created by the new
site before the squeeze happens.
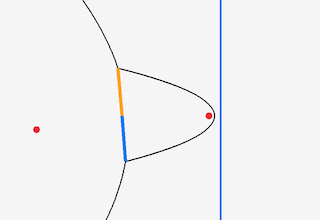
A couple of sections ago I started adding those orange lines to the diagram to indicate the equiedges, but I didn’t talk about what they were exactly. They ultimately become the (half) edges of the Voronoi. But they start out as incomplete edges. These are edges where one end is a fixed point, but the other is the intersection of two arcs. That intersection isn’t a fixed point, but changes depending on where the sweep line is. Hence why it’s incomplete: because one of the ends isn’t fixed yet.
We create two new incomplete edges whenever we put a new arc on the
beachline. The fixed point of both is the coordinate where the new arc
intersected the old one. And the arc-intersection are the two
intersections between the new arc and the one that it splits. If the new
arc is j and the old one is i, the arc-intersections
are [i,j] and [j,i].
## From the process_site_event function
new_arc = # the new site event we're processing
old_arc = # the old arc which is being split
fix = [calc_x(old_arc, new_arc.y, new_arc.x), new_arc.y]
incomplete_edges[PointPair{old_arc, new_arc}] = fix
incomplete_edges[PointPair{new_arc, old_arc}] = fixIn these pictures, I’ve put one of the incomplete edges in orange, and the other in blue, to make it clear there are two. You can see how the ‘center’ stays in the same place, but the other side changes with the sweep line.
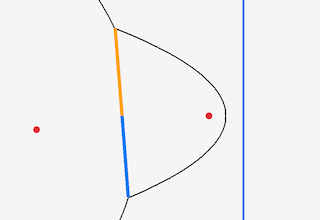
When two incomplete edges collide (during a circle event), the point of collision becomes a Voronoi Vertex, and the incomplete edges turn into half edges. Also a new incomplete edge is created where the fixed point is the Voronoi Vertex.
## From the process_circle_event function
mid_arc = # the arc that is getting squeezed
up_arc = # the arc that above it in the beachline
down_arc = # the arc that below it in the beachline
add_vertex(vd, center_of_circle)
fix1 = incomplete_edges[PointPair{up_arc, mid_arc}]
add_half_edge(vd, center, fix1)
fix2 = incomplete_edges[PointPair{mid_arc, down_arc}]
add_half_edge(vd, center, fix2)
# The new incomplete represents the new intersection
ft.incomplete_edges[PointPair{up_arc, down_arc}] = centerIn these pictures, you can see the incomplete edges ‘completing’ into half edges (colored black), and the new incomplete edges coming out of the intersection point.
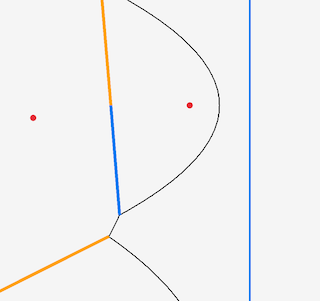
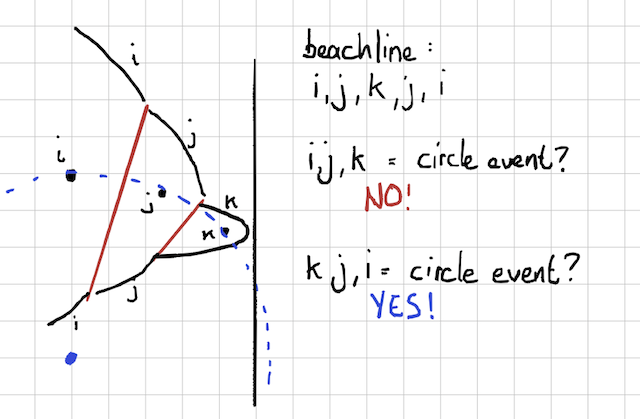
Look at this example. We’ve just processed the site k, and we have a
beachline [i,j,k,j,i]. We have the new potential circle
events ijk and kji. One of them is a circle
event. One of them is not a circle event. Scanning it visually,
it’s pretty obvious: The arcs at the top half of the picture,
ijk, will never have the middle arc squeezed, because the
lines are diverging. The arcs at the bottom half of the picture,
kji, clearly are going to converge, at the center of the
circle. So kji does create a circle event, but
ijk will not.
While it’s easy to see this visually, determining it programatically
is less intuitive. The trick is to realise that, when you read off the
points of the circle as ijk, they are going
clockwise around the circle. And if you read them as
kji, they are going counterclockwise. And this is test you
need to apply. You can do this by finding the determinant of the
points8
8 https://en.wikipedia.org/wiki/Curve_orientation
.
A negative determinant means a counterclockwise orientation (and so a
circle event). A positive one means a clockwise one (and so no circle
event). A determinant of zero means the points are in a straight line
(no circle!)
OK, so we have everything we need to do the algorithm now. To summarize the whole thing:
[..,i,j,k,..][..,i,j,L,j,k,..].[..,h,i,j,k,l,..][..,h,i,k,l,..].A bit of housekeeping: a V2 is a [2]int. A
PointPair is a pair of V2s, i.e. a
[2][2]int.
An Event is a struct of {site:bool, a,b,c:V2}. The
boolean indicates what type of event it is: a site (true) or circle
(false). The three V2s have different semantics depending
on the event. If it’s a site, then a is just the
coordinates of the site, and the other two are unused. If it’s a circle,
then the three V2’s are the arcs in the beachline that generated the
event. Or put another way, the three sites that site on the perimeter of
the the circle.
For the algorithm itself, we need to store the following things:
queue is an array of Events. Technically it’s
better to have this as a priority queue, but it’s not really important
to the implementation of the algorithm.beachline is an array of V2s. Again,
for efficiency you this implement this as a binary tree.incomplete_edges is a dictionary/map of
PointPair->V2This is the code, written in the wonderful C alternative Odin. The comments should hopefully explain what is being done and why where it’s not clear from the code9 9 There are a couple of other namespaces, mainly the detail of the math. These are in the code repo at https://github.com/RedPenguin101/voronoi .
package voronoi
import "core:math"
import "core:log"
/* Events can be site or circle events. site events are defined by a
single point, stored in a circle event are defined as the three
site points which define them. They are stored in a,b and c
respectively */
Event :: struct {site:bool, a,b,c:V2}
event_x_coord :: proc(e:Event) -> int {
if e.site do return e.a.x
else {
_,_,cp := circle_point(e.a,e.b,e.c)
return cp.x
}
}
event_y_coord :: proc(e:Event) -> int {
if e.site do return e.a.y
else {
_,_,cp := circle_point(e.a,e.b,e.c)
return cp.y
}
}
PointPair :: [2]V2
/* An "Incomplete Edge" is an edge between a point (which doesn't
change) and the intersection of two parabola defined by two focus
points (which does change, with the directrix). These will
ultimately become the half-edges of the DCEL, when two such
intersections meet.
The meaning of the fixed point - which I'll call the reference - is
different depending on what created it. The pair of incomplete
edges created by a site event start at the point at which the site
arc intersected the beachline. So it's sort of like the midpoint of
the edge (though not literally in the middle). If it's created by a
circle event, the fixed point is the vertex in the VD which was
created by that circle event. */
Fortune :: struct {
beachline:[dynamic]V2,
queue:[dynamic]Event,
incomplete_edges:map[PointPair]V2,
vd:DCEL,
}
add_site_event :: proc(q:^[dynamic]Event, v:V2) -> int {
return add_event_ordered(q, Event{true, v, {},{}})
}
add_circle_event :: proc(q:^[dynamic]Event, a,b,c:V2) -> int {
return add_event_ordered(q, Event{false, a,b,c})
}
add_event_ordered :: proc(queue:^[dynamic]Event, ev:Event) -> int {
// inserts an event into the queue by it's x value
if len(queue) == 0 {
append(queue, ev)
return 0
}
this_x := event_x_coord(ev)
for i in 0..<len(queue) {
other := queue[i]
other_x := event_x_coord(other)
if this_x == other_x {
this_y := event_y_coord(ev)
other_y := event_y_coord(other)
if this_y == other_y {
// We just ignore this duplicated event
return i
} else if this_y < other_y {
inject_at(queue, i, ev)
return i
}
}
else if this_x < other_x {
inject_at(queue, i, ev)
return i
}
}
append(queue, ev)
return len(queue)-1
}
initialise_fortune :: proc(f:^Fortune, sites:[]V2) {
clear(&f.beachline)
clear(&f.queue)
clear(&f.incomplete_edges)
clear_vd(&f.vd)
for site in sites do add_site_event(&f.queue, site)
}
process_site_event :: proc(ft:^Fortune, e:Event) -> int {
site := e.a
/* We need to check if this site is within the radius of any
upcoming circle events, because this will cause them to be
cancelled (a 'false alarm'). */
i:=0
for i < len(ft.queue) {
cev := ft.queue[i]
if !cev.site {
ctr, r, cp := circle_point(cev.a, cev.b, cev.c)
/* Adding 1 makes it a bit more conservative */
test := f32(r)+1.1
ed := euclid_distance(ctr, site)
if ed < test {
ordered_remove(&ft.queue, i)
i -= 1
}
}
i += 1
}
/* Trivial case of an empty beachline - just add it */
if len(ft.beachline) == 0 {
append(&ft.beachline, site)
return 0
}
/* Walk the beachline from top to bottom, for each arc checking
the y coordinate of the intersection with the following arc to see
if it's greater than our site y. The first arc that meets this
condition is the one which our new site will split. I set
insert_after as len-1, so it'll insert at the end if there is
none.*/
d := site.x
insert_after := len(ft.beachline)-1
for i in 0..<len(ft.beachline)-1 {
b, _, _ := intersection(ft.beachline[i], ft.beachline[i+1], d)
if b.y > site.y {
insert_after = i
break
}
}
/* The site is inserted into the beachline, and a copy of the arc
is inserted after that. This has the effect of 'splitting' the
arc, so if the beachline is abCde, where C is intersected arc,
after this operation it will be acCSCde, where S is the new site
we're adding. This creates two new intersections: Between CS and
SC */
arc := ft.beachline[insert_after]
inject_at(&ft.beachline, insert_after+1, site)
/* We have to handle the special case where the arc and site have
the same x coordindate, and therefore have only one intersection*/
same_x := arc.x == site.x
if !same_x do inject_at(&ft.beachline, insert_after+2, arc)
/* Calculate the point at which a horizontal line from the new
site intersects the arc. This becomes the reference point for two
incomplete edges, one for each of the new intersections we
created. by inserting the new arc into the beachline.*/
ref := V2{calc_x(arc, site.y, site.x), site.y}
/* Once more, we need to handle the special case of equal xs. We
create the reference point off-map so it will be properly cleaned up*/
if same_x do ref = {-1, (site.y+arc.y)/2}
if !same_x {
ft.incomplete_edges[PointPair{site, arc}] = ref
}
ft.incomplete_edges[PointPair{arc, site}] = ref
/* Check the new arc against the two arcs above it and below it in
the beachline to see if there are any new circle events we need to
add to the queue */
new_arc_idx := insert_after+1
if new_arc_idx >=2 do new_circle_event(ft, new_arc_idx-2)
if new_arc_idx <= len(ft.beachline)-3 do new_circle_event(ft, new_arc_idx)
return new_arc_idx
}
circle_point :: proc(a,b,c:V2) -> (center:V2, radius:int, circle_point:V2) {
/* Given three points, calculate the circumcircle which passes
through all three points. It returns the center and radius of the
circle, as well as the circle-point, that being the right-most
point of the circle.
https://en.wikipedia.org/wiki/Circumcircle
*/
/* normalize on a */
b := b-a
c := c-a
D := f32(2*(b.x*c.y-b.y*c.x))
u:V2f
u.x = f32(c.y*(b.x*b.x+b.y*b.y)-b.y*(c.x*c.x+c.y*c.y))
u.x /= D
u.y = f32(b.x*(c.x*c.x+c.y*c.y)-c.x*(b.x*b.x+b.y*b.y))
u.y /= D
r := math.sqrt(u.x*u.x + u.y*u.y)
ui := V2f_to_i(u)+a
return ui, int(r), ui+V2{int(r), 0}
}
new_circle_event :: proc(ft:^Fortune, start_at:int) -> int {
assert(start_at >= 0)
assert(len(ft.beachline) > start_at+2)
/* A circle event is created if three sites in a beachline sit on
counterclockwise circle, which is what taking the determinant
checks. Basically, if the points i,j,k are counterclockwise, the
lines defined by equipoints of i,j and j,k will converge, and if
they are clockwise (or they sit on a straight line, with a
determinant of zero), they won't.
It's important to check this, because consider the beachline
ijkji. Both ijk and kji will form a circle, but only one will be
valid.*/
h:=ft.beachline[start_at]
j:=ft.beachline[start_at+1]
k:=ft.beachline[start_at+2]
det := (j.x-h.x)*(k.y-h.y)-(j.y-h.y)*(k.x-h.x)
if det < 0 {
return add_circle_event(&ft.queue, h,j,k)
}
return -1
}
process_circle_event :: proc(ft:^Fortune, e:Event) -> int {
assert(!e.site)
center, r, cp := circle_point(e.a, e.b, e.c)
/* As with the site event, we iterate through the beachline to
find the appropriate arc to select for removal. In this case, the
arc to remove is the middle one of the three points which describe
the circle event. So we can just iterate through the beachline
checking for that sequence.*/
rmv := len(ft.beachline)-1
for i in 0..<len(ft.beachline)-2 {
h := ft.beachline[i]
j := ft.beachline[i+1]
k := ft.beachline[i+2]
if h == e.a && j == e.b && k == e.c {
rmv = i+1
break
}
}
if rmv < 1 || rmv >= len(ft.beachline)-1 {
return rmv
}
mid_arc := ft.beachline[rmv]
up_arc := ft.beachline[rmv-1]
down_arc := ft.beachline[rmv+1]
/* When two arcs (the up and down arcs) squeeze a third arc (the
middle arc), the point at which they meet becomes a vertex in the
VD.
It also causes the incomplete edge which we are tracking between
up and mid, and mid and center, to crystalize into the half edges.
*/
add_vertex(&ft.vd, center)
ref1 := ft.incomplete_edges[PointPair{up_arc, mid_arc}]
delete_key(&ft.incomplete_edges, PointPair{up_arc, mid_arc})
add_half_edge(&ft.vd, center, ref1)
delete_key(&ft.incomplete_edges, PointPair{up_arc, mid_arc})
ref2 := ft.incomplete_edges[PointPair{mid_arc, down_arc}]
add_half_edge(&ft.vd, center, ref2)
delete_key(&ft.incomplete_edges, PointPair{mid_arc, down_arc})
/* A new incomplete edge is created between the up and down arcs,
with the reference point being the center of the circle (i.e.
where the three arcs intersected)
We need to handle the special case that the site IS the circle
point. This indicates that point the site hits the beachline is at
the exact meeting point of two arcs */
ref3 := center
midpoint := (up_arc+down_arc)/2
if center == ref1 || center == ref2 {
ref3 = midpoint
}
if midpoint == ref1 || midpoint == ref2 {
// Very unlucky
ref3 += {1,1}
}
add_half_edge(&ft.vd, center, ref3)
ft.incomplete_edges[PointPair{up_arc, down_arc}] = ref3
/* we remove the arc from the beachline */
/* Collapsing the arc can invalidate future events which have that
arc as part of it. Here we check every future event to see if it's
now invalid. This is very inefficient, there should be faster way
to do this */
// TODO Find a more efficient way to do this
i := 0
r0 := ft.beachline[rmv-1]
r1 := ft.beachline[rmv]
r2 := ft.beachline[rmv+1]
for i < len(ft.queue) {
ev := ft.queue[i]
if !ev.site {
if ev.b == r0 && ev.c == r1 || ev.a == r1 && ev.b == r2 {
ordered_remove(&ft.queue, i)
i -= 1
}
}
i += 1
}
ordered_remove(&ft.beachline, rmv)
/* Collapsing the arc has possibly created a new circle event. If
the beachline as abCde before, and we removed C, we need to check
abd, and bde for new circle events. Since we removed C, the
'to_remove' index (i) is now pointed at d, so that means checking
i-2, i-1, i for the up direction, and i-1, i, i+1 in the down
direction. */
if rmv >=2 do new_circle_event(ft, rmv-2)
if rmv >= 1 && rmv <= len(ft.beachline)-2 do new_circle_event(ft, rmv-1)
return rmv
}
clean_beachline_edges :: proc(ft:^Fortune, d:int) {
/* As the sweepline advances, the arcs on each end of the can
become overtaken by those further toward the middle. If the bottom
of the beachline ends with arcs ijk, if the midpoint of jk is no
longer in bounds of the digram, it's pruned off.*/
l := len(ft.beachline)
/* A beachline of length 0 or 1 has nothing to prune */
if l < 2 do return
mp : V2
mp = (ft.beachline[0]+ft.beachline[1])/2
b, _, sols := intersection(ft.beachline[0], ft.beachline[1], d)
if b.y < 0 {
_,vv,_ := line_rectangle_intersection(mp, b)
ordered_remove(&ft.beachline, 0)
l -= 1
}
if l < 2 do return
mp = (ft.beachline[l-1]+ft.beachline[l-2])/2
_, b, sols = intersection(ft.beachline[l-1], ft.beachline[l-2], d)
if sols == 2 && b.y > H {
_,vv,_ := line_rectangle_intersection(mp, b)
ordered_remove(&ft.beachline, l-1)
}
}
calc_vd :: proc(sites:[]V2, ft:^Fortune, max_x:=W) {
initialise_fortune(ft, sites)
/* While there are events in the queue, process them. */
final_x := 0
for len(ft.queue) > 0 {
ev := ft.queue[0]
final_x = event_x_coord(ev)
if max_x != -1 && event_x_coord(ev) > max_x do return
ordered_remove(&ft.queue, 0)
clean_beachline_edges(ft, event_x_coord(ev))
if ev.site do process_site_event(ft, ev)
else do process_circle_event(ft, ev)
}
clear(&ft.beachline)
/* For any incomplete edges that remain, calculate where they
intersect the diagram side and create edges at those points. */
for is, ref in ft.incomplete_edges {
if inbounds(ref) {
p , _,_ := intersection(is.x, is.y, max(W*2, final_x*2))
_,le,_ := line_rectangle_intersection(ref,p)
add_half_edge(&ft.vd, le, ref)
add_vertex(&ft.vd, le)
}
delete_key(&ft.incomplete_edges, is)
}
complete_vd(&ft.vd)
}One of the difficulties implementing this algorithm is that there’s lots of fiddly edge cases to consider. I’m not going to go into all the ones I found, because they are quite tedious. And there are probably many that I missed.
Another topic I haven’t covered is the datastructure for a Voronoi: The Doubly Connected Edge List or DCEL. There’s a bit at the end about them, but they are neither very interesting nor core to the algorithm.
There is one procedure I didn’t talk about in the algorithm called ‘cleaning the beachline’, which just looks at two ends of the beachline and prunes off any uneccessary arcs.
Finally, that last step - what to do after the queue is empty - I haven’t gone into detail about. It involves a bit of simple math to go through all the incomplete edges, untwinned half edges, and vertices and just tidy them up a bit. Again, not very interesting.
Voronois are usually stored in a doubly-connected-edge-list (DCEL). This data structure describes a ‘web’ of vertices and edges between those vertices (called a cell-complex, which is what a Voronoi technically is) in a way that’s easy to manipulate and transform.
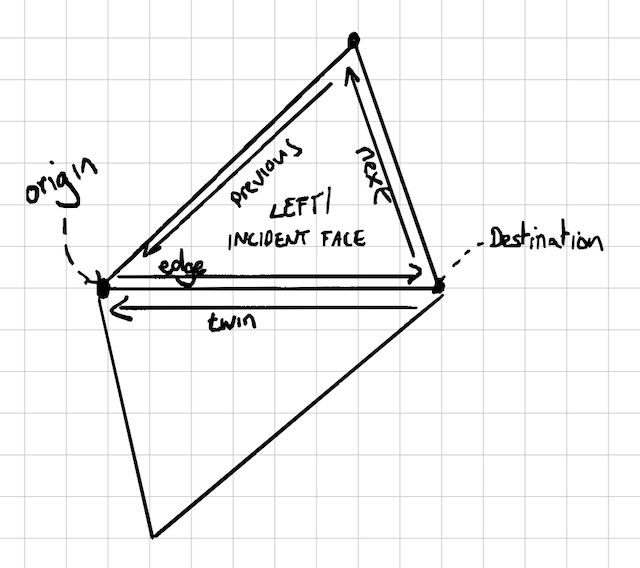
DCEL is a primarily edge-based representation, but it also stores the vertex and face information. Edges in a cell-complex are undirected, but in a DCEL each edge is stored as two directed ‘half edges’, one in each direction. In the case of the Voronoi diagram, the stored vertices are not the sites, but the Voronoi vertices. The structure is like this:
DCEL:
Edge[]:
twin, next, previous:^Edge,
origin:^Vertex
left:^Face
Vertex[]:
ID:int,
Coord:V2,
incident:^Edge
Face[]:
incident:^EdgeThe ‘twin’ of the edge going from vertex A to B is the vertex going
from B to A. If we store the origin of the edge, we can get to the
destination by E.twin.origin. And similarly, we store the
left face, but to get to the right face we do E.twin.left.
The edge pointer on the vertex can be to any edge which has this vertex
as its origin.